Multiplication is the operation that finds the total number of items when equal groups are combined, so it shortens repeated addition into a single step. Teachers launch lessons with arrays of dots, equal rows of chairs, or sets of jump-rope skips to show that factors tell how many groups and how many items are in each group. When students see 4 × 6, they learn that the first factor describes four groups and the second factor describes six objects in each group. Rewriting 4 × 6 as 6 + 6 + 6 + 6 proves why multiplication saves time. Number lines, area models, and bar diagrams let students trace jumps or shaded squares to see the structure.
The base-ten system and place value charts help students move from repeated addition to partial products. A two-digit by one-digit problem becomes manageable when tens and ones are decomposed, so 23 × 4 turns into (20 × 4) + (3 × 4). Once students master partial products, they explore multi-digit algorithms that stack numbers, line up place values, and regroup as needed. Skip-counting songs, multiplication tables, and flash-card games build fact fluency so students can focus on reasoning rather than counting. Teachers also stress that multiplication is everywhere, from measuring area to computing ingredient amounts in recipes.
Multiplication has properties that make complex problems easier. The commutative property shows that switching factors does not change the product, so 5 × 7 = 7 × 5. The associative property allows grouping factors differently without changing the result, such as (2 × 3) × 4 = 2 × (3 × 4). The distributive property connects multiplication with addition or subtraction, helping students break apart large factors into friendlier pieces. These properties support mental math strategies like doubling and halving or using known squares to tackle new facts. Understanding why these shortcuts work builds flexible thinking for algebra later on.
Real-life multiplication explains how many seats are in a theater, how many pages a printer produces in an hour, or how much fencing surrounds a garden. Scientists multiply rates to find speed or energy, while shop owners multiply prices by quantities to set totals. Multiplication also underlies patterns, sequences, and scaling. Estimation methods such as rounding factors or using compatible numbers give students a quick sense of the product’s size before computing exactly. Checking answers might include reversing factors, using division, or comparing to repeated addition to ensure the product fits the situation.
Practice stays engaging through games, digital tools, and projects. Students build multiplication mosaics with graph paper, design equal group stories, or solve puzzles that require matching factors to arrays. Mental math warm-ups ask them to find 25 × 4 by doubling twice or to multiply by ten before adjusting. Teachers encourage neat organization, clear labeling of units, and explanations of how each step relates to the original problem. Multiplication opens doors to division, fractions, ratios, and algebra, so confidence with factors and products supports every future math adventure.
Multiplication
Level
readlittle.com
Combining equal groups efficiently
What We Can Learn
- Multiplication shortens repeated addition by combining equal groups in one step.
- Arrays, number lines, and area models show how factors and products relate.
- Properties of multiplication create flexible strategies for multi-digit problems.
- Real-life rates, measures, and budgets rely on accurate multiplication.
Related Reads

Divisibility rule
Shortcuts for spotting factors

Long division
A step-by-step algorithm for multi-digit division

Arithmetic
Everyday math for smart counting

Addition
Joining numbers to make a sum
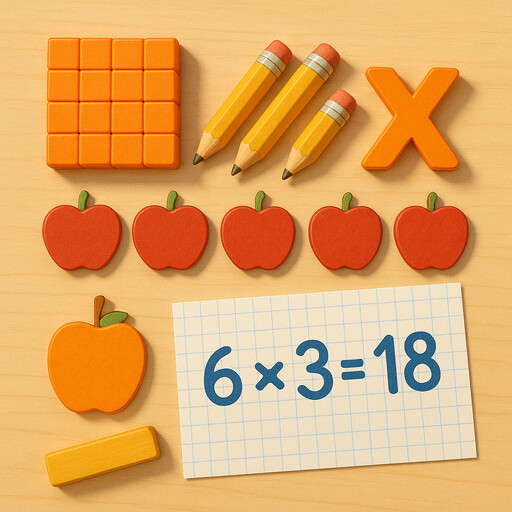
Subtraction
Finding what remains when amounts change
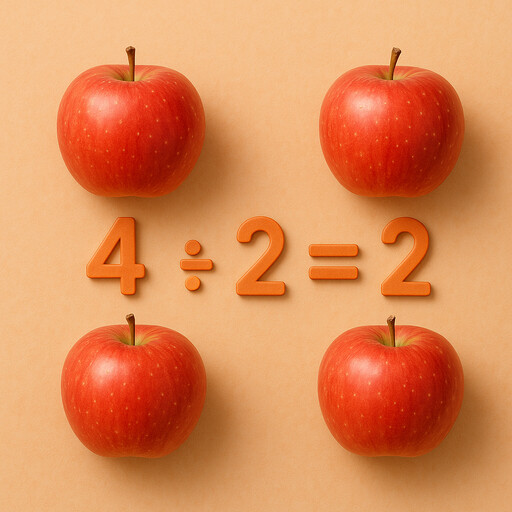
Division
Sharing and measuring with equal groups
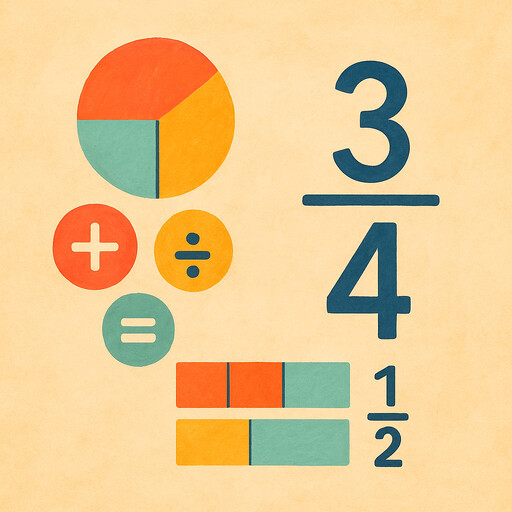
Fraction
Equal parts of a whole

Decimal
Base-ten numbers with fractional parts