Divisibility rule is a quick test that tells whether one number divides another without performing the full division. These rules help students identify factors, simplify fractions, and determine whether numbers are prime or composite. For example, a number is divisible by 2 if its last digit is even, and divisible by 5 if it ends in 0 or 5. Teachers present the rules as puzzles, encouraging students to justify why each rule works before memorizing it.
Common divisibility rules cover small integers. A number is divisible by 3 if the sum of its digits is divisible by 3. Divisibility by 9 uses the same method but with nine. A number is divisible by 4 if its last two digits form a number divisible by 4, and divisible by 8 if the last three digits form a multiple of 8. Divisibility by 6 requires the number to be divisible by both 2 and 3. These patterns rely on place value and base-ten structure.
More advanced rules apply to numbers like 7, 11, or 12. For 11, students subtract and add alternating digits; if the result is divisible by 11, the original number is too. The rule for 7 involves doubling the last digit, subtracting from the remaining number, and repeating the process. Rules for 12, 15, or 25 combine earlier tests. Teachers encourage students to create their own explanations or proofs using algebraic expressions to deepen understanding.
Divisibility rules help with many tasks. Students factor numbers quickly, reduce fractions, and verify solutions to multiplication and division problems. When finding greatest common factors or least common multiples, divisibility rules cut down the amount of trial and error. They also support mental math and estimation because students can recognize multiples without long calculation. Games and scavenger hunts challenge learners to classify numbers by divisibility in fun ways.
Real-life contexts include sorting serial numbers, checking barcodes, designing coding puzzles, and analyzing data sets. Mathematicians and computer scientists use divisibility tests within algorithms that handle large numbers. Learning these rules builds number sense, logical reasoning, and confidence before students tackle algebra and number theory. Divisibility rules turn patterns in place value into powerful shortcuts for solving problems.
Divisibility rule
Level
readlittle.com
Shortcuts for spotting factors
What We Can Learn
- Divisibility rules provide fast tests for determining whether numbers divide evenly.
- Patterns based on digit sums or last digits explain divisibility for 2, 3, 4, 5, 6, 8, and 9.
- Advanced rules for numbers like 7, 11, and 12 build on simpler tests.
- Factoring, simplifying fractions, and coding all benefit from divisibility shortcuts.
Related Reads
Prime number
Numbers with only two factors

Long division
A step-by-step algorithm for multi-digit division

Arithmetic
Everyday math for smart counting

Addition
Joining numbers to make a sum
Subtraction
Finding what remains when amounts change
Multiplication
Combining equal groups efficiently
Division
Sharing and measuring with equal groups
Fraction
Equal parts of a whole

Decimal
Base-ten numbers with fractional parts
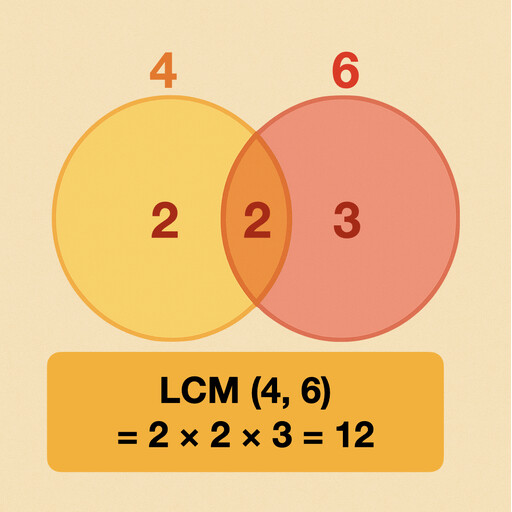
Least common multiple
The smallest shared multiple of numbers
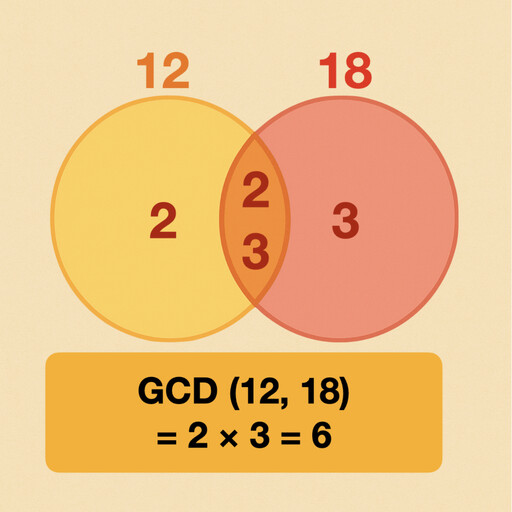
Greatest common divisor
The largest number dividing others evenly

Rhythm
Regular patterns of sound and movement