Prime number is a whole number greater than 1 that has exactly two factors: 1 and itself. The smallest prime is 2, which is also the only even prime. Teachers introduce primes by exploring arrays, factor pairs, and divisibility tests so students can see how composite numbers have more than two factors. Sieve of Eratosthenes activities let learners shade multiples on a grid to discover primes visually.
Understanding prime numbers strengthens multiplication and division skills. Students list factors of numbers like 12 and compare them to the factors of 13 to notice the difference between composite and prime. Prime factorization expresses any whole number as a product of primes, such as 60 = 2^2 × 3 × 5. This method supports simplifying fractions and finding greatest common factors or least common multiples. Teachers emphasize that 1 is not prime because it has only one factor.
Primes also appear in patterns and modern technology. Cryptography uses very large primes to create secure codes for digital information. Computer scientists develop algorithms to search for new primes, and mathematicians investigate twin primes and other conjectures. Students analyze sequences of primes to look for patterns, even though the gaps between primes grow irregularly. Real-life contexts include real-time encryption for banking, messaging, and online shopping.
Practice with primes includes sorting cards, playing factor games, and building prime towers with blocks. Students use divisibility rules for 2, 3, 5, 9, and 10 to decide quickly whether a number might be prime. Graphs showing the density of primes invite discussion about how primes become less frequent but never stop. Working with primes improves number sense and prepares learners for algebra and number theory.
Primes inspire curiosity because they seem simple yet mysterious. They form the “atoms” of multiplication, and every composite number can be broken back down into prime building blocks. Exploring primes encourages persistence, pattern recognition, and logical reasoning. Whether counting marbles or securing messages, prime numbers play an essential role in mathematics.
Prime number
Level
readlittle.com
Numbers with only two factors
What We Can Learn
- Primes are greater than 1 and have only two factors: 1 and themselves.
- Prime factorization breaks composite numbers into prime building blocks.
- Divisibility rules and number patterns help identify primes efficiently.
- Cryptography and coding rely on large prime numbers for security.
Related Reads

Divisibility rule
Shortcuts for spotting factors

Arithmetic
Everyday math for smart counting

Addition
Joining numbers to make a sum
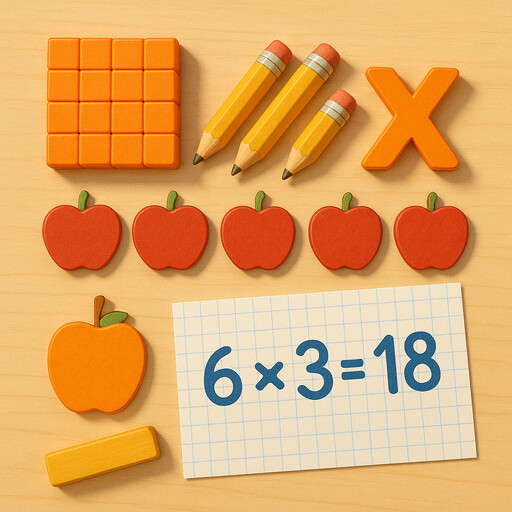
Subtraction
Finding what remains when amounts change
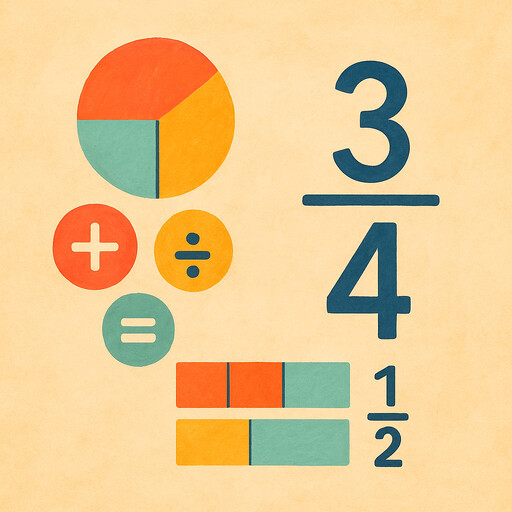
Fraction
Equal parts of a whole
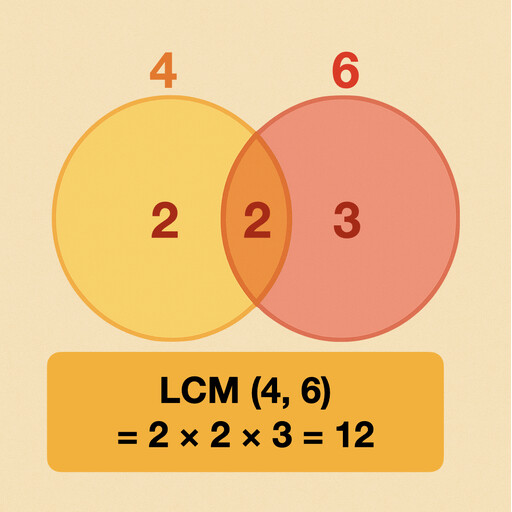
Least common multiple
The smallest shared multiple of numbers
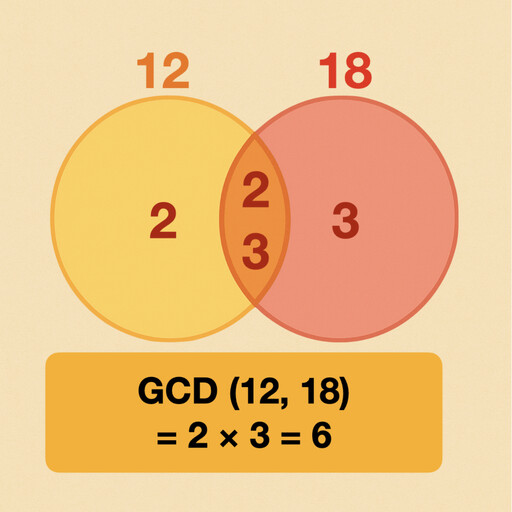
Greatest common divisor
The largest number dividing others evenly

Rhythm
Regular patterns of sound and movement
Large language model
AI system that understands and generates text

Mathematics
The universal language of numbers and patterns